準結晶の電子状態
これまでの物性物理学（固体物理学）では、固体の性質を結晶構造の周期的性質（並進対称性）に基づいて理解してきました。
準結晶はこの大前提に当てはまらない、並進対称性を持たないにもかかわらず高い秩序度（準周期）を持った固体です。
物質の熱・電気・弾性等のほとんどの物理的性質は、物質中の電子状態によって決定されます。
結晶中の電子状態は、ブロッホ波と呼ばれる結晶の周期的性質の影響を受けた波の状態を取ります。
この考え方は、周期性を持たない準結晶においては全く通用しません。
準結晶の理的性質を理解するためには、周期性を仮定している教科書の1ページまで立ち戻って理解を修正する必要があります。
周期と準周期の違いについて、簡単な例で理解してみましょう。
ここでは、LとSという仮想的な原子が集まって結晶を構成しているとします。
通常の結晶の場合は、ある方向に向かって、例えば、
(a) LSLSLSLSLSL… 、 (b) LSLLSLLSLLSLLS… 、(c) LSLLSLSLLSLSLLS…
の様に周期的に並んでいます。
この周期的な構造を理解すれば、任意の位置の原子を知ることができます。
例えば、それぞれの配列で左から100番目にはLかSのどちらが来るでしょうか？
これは並進対称性という性質であり、この配列を左右に(a)は2個ずつ、(b)は3個ずつ、(c)は5個ずつ動かしても、移動の前後で区別が付かないことを表しています。
準周期には並進対称性はありません。
しかし高い秩序度を持つために、任意の位置の原子が何であるかを知ることができます。
一見して矛盾するようなこの性質は、準周期の例であるフィボナッチ数列を用いた構造で理解することができます。
この準周期は以下の様なルールで生成できます。
1．最初は L 一つだけから始める。
2．L --> LS, S --> L の変換を同時に行う。
この変換を無限に繰り返すことで、以下の様にLとSは周期的ではないものの高い秩序を持って準周期的に整列します。
L --> LS --> LSL --> LSLLS --> LSLLSLSL --> LSLLSLSLLSLLS --> …
（左から100番目にはLかSのどちらが来るでしょうか？）
この各ステップでのL(もしくはS)の数は(0), 1, 1, 2, 3, 5, 8,… となり、フィボナッチ数列を形成します。
2次元の準周期系としてはペンローズタイル等が知られており、我々の存在する3次元空間においても様々な合金系に準結晶が存在します。
さらに、これらの準周期系は高次元における周期結晶の投影として理解できることが知られています。
我々の研究グループでは、高度な極限環境測定技術を生かして準結晶の電子状態や秩序状態を調べる研究を行っています。
図1は2018年に発見された準結晶で初めて超伝導が発見された際の電気抵抗と比熱の異常を発見したデータです。
これらは我々の研究グループのミリケルビンでの極低温測定技術を用いて測定を行いました。
このデータで示す様な 30mK 付近までの極低温で比熱を測定できる研究グループは極めて限られます。
準結晶における超伝導の発見は、準周期構造における長距離秩序が見つかった初めての例でもあります。
準周期系においては今も様々な分野の研究者が活発な研究を行っており、新しい発見が次々と相次いでいます。
我々の持つ極限環境測定技術を生かすことで、準結晶系の長距離秩序や電子状態の性質を明らかにすることを目指しています。
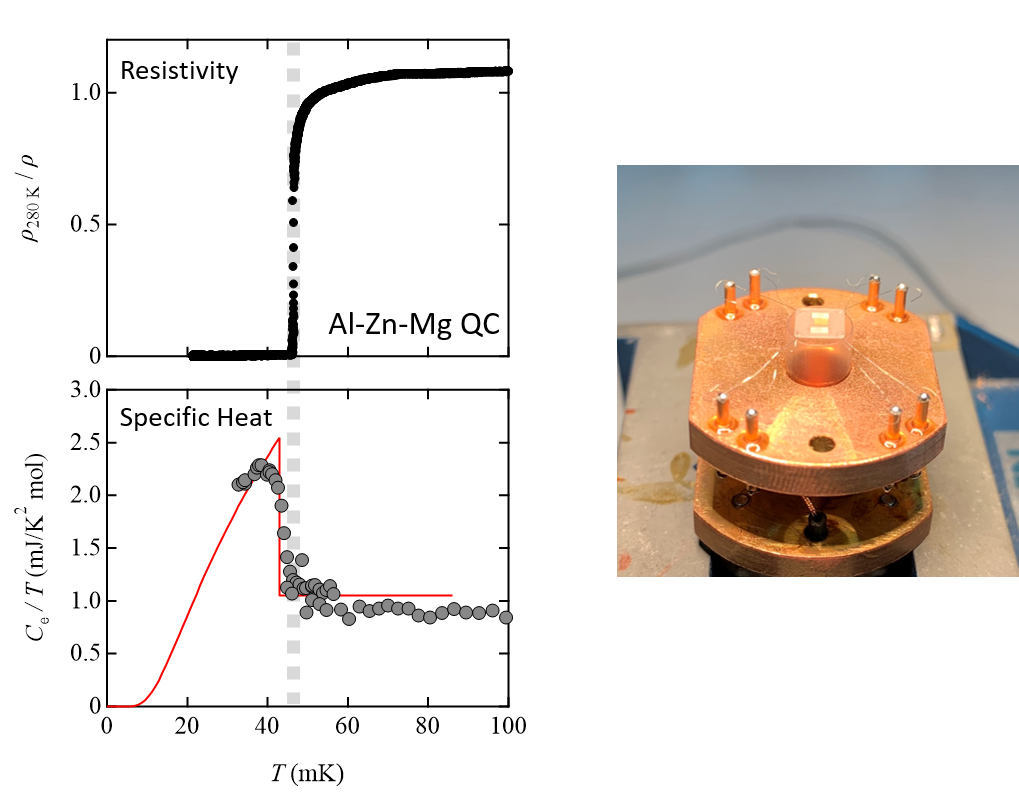図1．(左) Al-Zn-Mg系準結晶の超伝導現象（名古屋大学と北海道大学との共同研究）
50 mK付近で電気抵抗がゼロになり比熱に跳びが現れることが超伝導発現の強い証拠となった。
(右) 実験に用いた自作の比熱測定装置。