パリティの破れに起因したフェルミ面のスピンテクスチャー
物質、とりわけ金属の電子状態を解明するうえで、フェルミ面と呼ばれる性質を調べることは重要とされています。我々はドハース・ファンアルフェン効果と呼ばれる磁化の量子振動現象を用いて、強相関伝導系のフェルミ面の性質を調べています。最近我々は、このドハース・ファンアルフェン効果で、空間反転対称性の破れた金属のフェルミ面間で生じる「軌道交差」という現象を見出しました。
初等的な固体物理の教科書では、電子のエネルギーバンドあるいはフェルミ面は、スピンの自由度を無視するか、あるいは「縮退」しているものとして扱っています。ところが、結晶の空間反転対称性が破れている物質では、反対称スピン軌道相互作用によって電子状態は2つのエネルギー状態に分裂します。この対称性の破れに起因した電子状態のスピン自由度による分裂は、たとえば図1(a)のように、大きさの異なる2つのフェルミ面となって現れます。このとき、スピンの向きは波数ベクトルに依存するようになりますが、このスピンの構造（スピンテクスチャー）を実験的にとらえるのは難しいとされています。
反対称スピン軌道相互作用によるフェルミ面の分裂は、結晶の対称性を考慮すると、特定の方向で再び縮退することがあります。このとき、フェルミ面に沿って運動するキャリアの軌道は、図1(b)のようにこの縮退点で「交差」することが可能になります。我々は、片方のフェルミ面からもう片方のフェルミ面に軌道が切り替わる「軌道交差」を実験的にとらえることに成功しました。
軌道交差の振動振幅からは、交差を起こす確率を見積もることができるのですが、その交差確率を決める要因はまだよくわかっていません。軌道交差ではスピン反転の有無が伴うことから、フェルミ面のスピン構造が影響している可能性もあります。今後の研究の発展が期待されます。
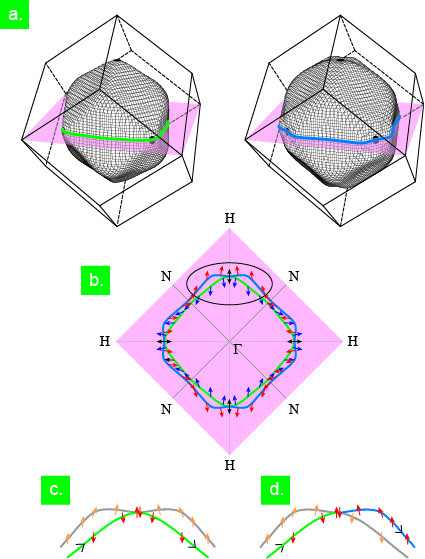
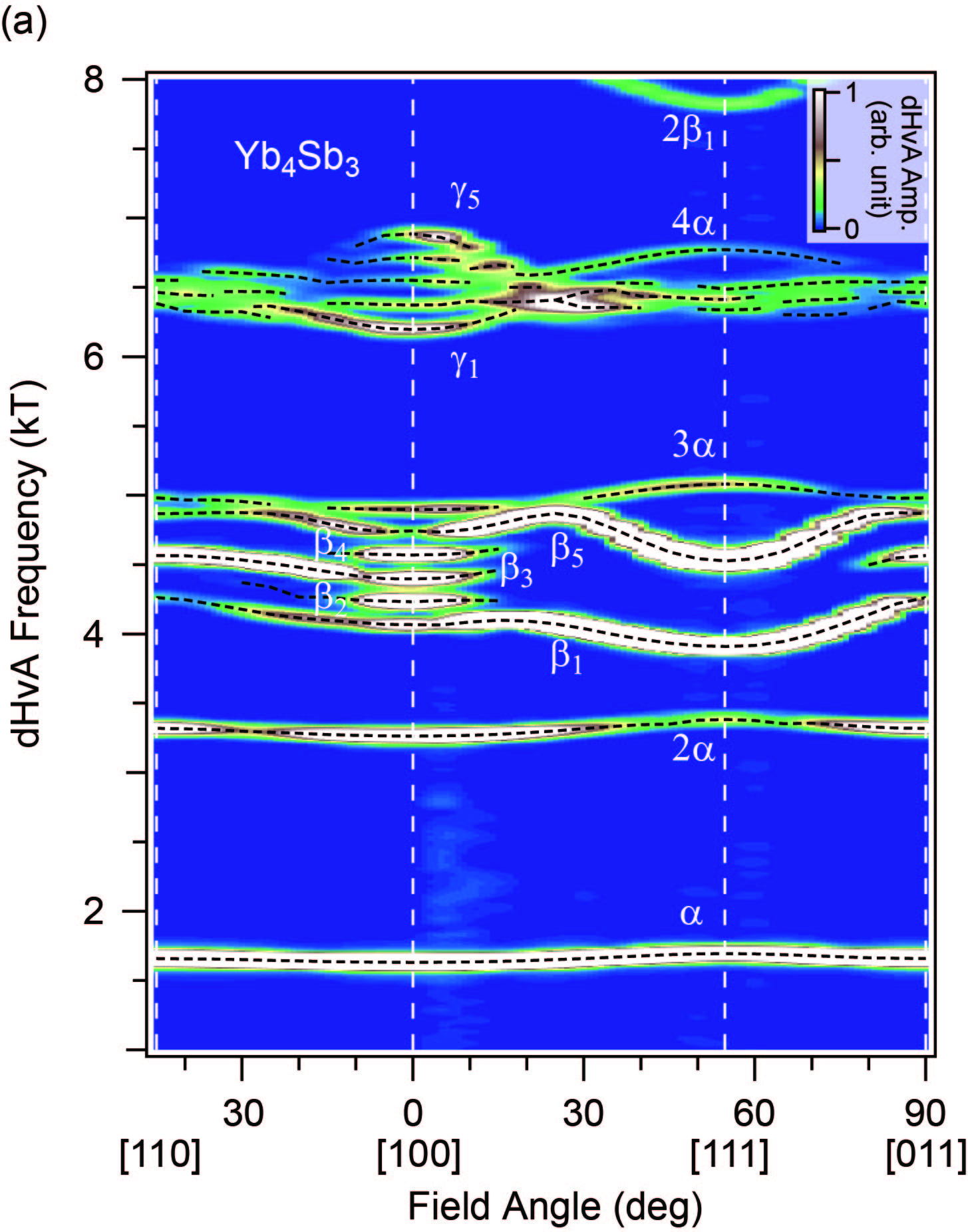図1．(左) 反対称スピン軌道相互作用によるフェルミ面分裂。
(a) 反対称スピン軌道相互作用によって分裂したフェルミ面。
(b) (a)のピンクで示した面（{100}面）でカットしたフェルミ面の断面。内側の軌道が緑、外側の軌道が青で示されている。黒い点はスピン縮退点。
(c) 内側を通る軌道と(d) 内側から外側に切り替わる軌道。矢印はスピンの向きを表す。
(右) 空間反転対称性の破れた金属(Yb4Sb3)のドハース・ファンアルフェン周波数の角度依存性。
振動振幅をカラーで表している。